[파이썬] 이진 탐색 알고리즘, 해시 탐색 알고리즘

15 Sep 2021

Reading time ~5 minutes

이진 탐색 Binary Search

데이터를 찾는 알고리즘 반드시 미리 오름차순이나 내림차순으로 정렬이 되어 있어야 한다. 탐색하는 범위를 절반씩 줄여 나가면서

이진 탐색 알고리즘

가운데 요소를 선택한다.
가운데 요소와 찾는 데이터를 비교한다.
탐색 범위를 절반으로 좁힌다.
찾는 데이터가 존재하지 않을 수도 있다.

가운데 요소를 선택하는 방법

평균을 이용해서 가운데 요소를 찾는다.
0 ~ 10 0+10/2 = 5
head tail (head+tail)/2
요소의 갯수가 짝수라면 0~5
0+5/2=2.5 보통 버리기를 사용한다.

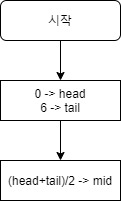
가운데 요소와 찾는 데이터를 비교한다. 가운데 요소가 정해지면 요소의 데이터와 찾는 데이터가 일치하는지 확인한다. 가운데 위치를 나타내는 첨자는 mid에 대입되어 있다. 항상 arrary[mid] 로 가운데 요소를 나타낸다. 예를 들어 array[mid] = 17 Yes라면 내가 찾는 값이 mid일치한다.

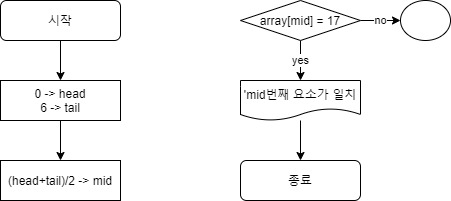
가운데 데이터와 원하는 데이터가 일치하지 않는 경우 No 케이스 , 원하는 데이터가 가운데 데이터 보다 크거나 혹은 작거나 두가지 경우 전부 탐색 범위의 절반으로 줄이는 처리로 이동한다.

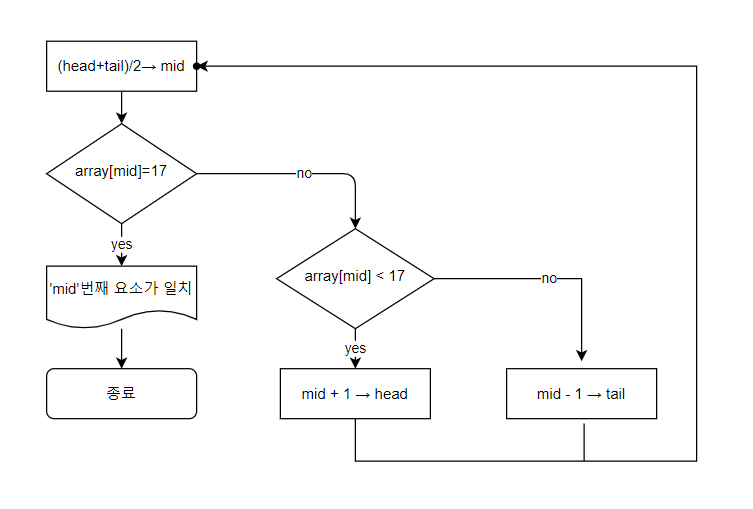
문제

아래 알고리즘을 보고, 파이썬 코드를 작성해보자!

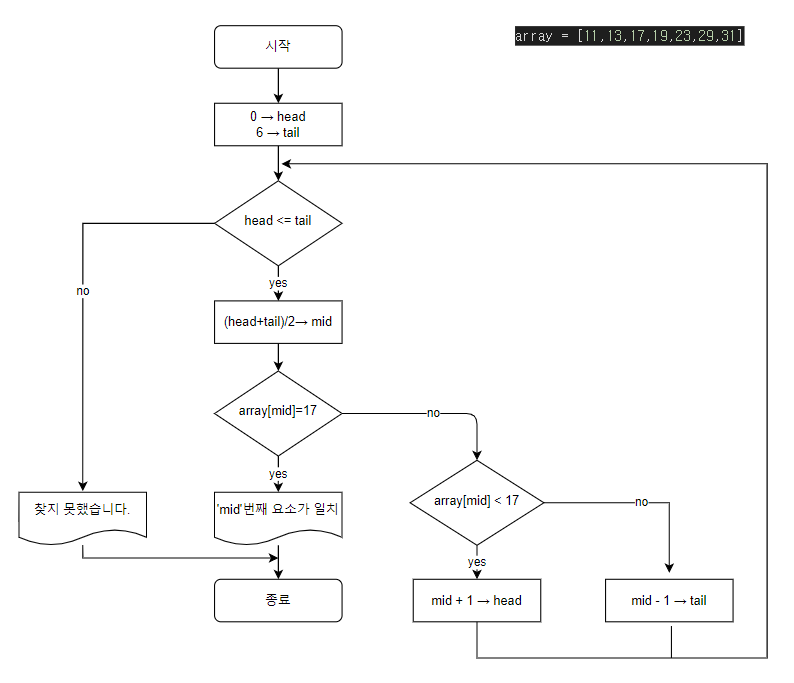
array = [11,13,17,19,23,29,31]

head = 0
tail = 6

while True:
  if head <= tail:
    mid = (head+tail)//2  # 소수점 이하가 나올수 있으니 몫만 취하자! 
    if array[mid] == 17: 
      print(mid,'번째 요소가 일치')
      break
    else:
      if array[mid] < 17:
        head = mid + 1
      else:
        tail = mid - 1

  else:
    print("찾지 못했습니다.")
    break

해시 탐색 알고리즘

데이터를 찾는 탐색 알고리즘
탐색하기 쉽게 미리 함수를 사용해서 데이터를 보관한다.
보관하는데 사용한 함수를 사용하여 단번에 찾을 수 있다.

해시탐색법의 특징

지금까지의 탐색법들은 원하는 데이터가 어떤 요소에 들어 있는지 전혀 모르는 상태에서 검색을 한다. 그러나 해시탐색법은 데이터의 내용과 저장한 곳의 요소(인덱스)를 미리 연계해 둠으로써 극히 짧은 시간안에 탐색할 수 있도록 고안된 알고리즘
해시탐색법은 ‘데이터를 데이터와 같은 첨자의 요소에 넣어두면 한번에 찾을 수 있다’라는 아이디어에서 시작된다.
예를 들면 24인 데이터를 24의 요소에 넣어두고 36의 요소에 넣어두는 방식이다.
확실히 쉽게 찾을 수 있지만 문제는 두개만 담아두려고 해도 37개의 요소를 가진 배열을 준비해야 한다. 이렇게 되면 낭비가 심해진다.
좀 더 효율적으로 배열을 사용하기 위해서 일정한 계산을 하여 그 계 방에 보관하는 방법을 생각해 볼 수 있다.
미리 탐색하기 쉽게 데이터를 보관하는 단꼐에서 사전 준비를 해 두는 것이 특징이다.
가장 알기 쉬운 방법은 데이터의 숫자와 같은 칸에 넣어 두는 것이다. 예를 들면 11,15,24,26 숫자들을 저장하기 위해서 26개의 칸을 준비하는 것은 극히 비효율적이다. 방을 7개만 준비하여 잘 배분하여 저장하기 위해서 나눗셈을 사용한다.
칸의 7개 준비한다. 어떤 숫자라도 7로 나누면 나버지는 0에서부터 6중 하나가 나오게 된다.
숫자들을 7로 나누어 그 나머지를 계산해보자.

제대로 흩어진 상태가 되었다. 각각의 데이터를 나머지 값과 같은 번호의 칸에 넣어둔다.
데이터를 넣을 칸의 번호 = 숫자 % 칸의 수
해시함수를 통해 산출된 값은 해시값

해시탐색법으로 데이터를 찾는 방법

11는 데이터를 찾아보자. 데이터를 찾을 때도 위에서 만든 해시함수를 다시 사용한다.
해시함수로 해시값을 구하는 계산식은 ‘공의 숫자 % 7’이다. 이 해시함수에 11을 넣어 계산하면 해시값은 4가 된다. 해시값은 데이터가 들어 있는 칸의 번호이다.
따라서 해시탐색법을 사용하면 단 한번의 계산으로 찾고자 하는 데이터를 찾을 수 있다.
해시함수를 사용하여 데이터를 저장하는 장소를 정해두어 검색 시간을 놀라울 정도로 단축시킬 수 있다는 큰 장점이 있다.

해시 함수로 데이터를 보관하는 알고리즘

해시함수는 데이터의 저장소 첨자를 계산하는데 사용된다.
저장소의 첨자가 겹치는 것은 ‘충돌’이라고 한다.
충돌이 발생하면 옆의 빈 요소에 데이터를 보관한다.

배열을 2개 준비한다. 데이터를 보관할 임시 배열(arrayD)을 준비한다. 첨자는 0~7를 사용하여 12,25,36,20,30,8,42 데이터를 임시 저장한다.
데이터를 최종 저장할 배열(arrayH)을 준비한다. 첨자는 0~10로 11개의 배열을 준비하여 기본값을 0으로 초기화한다.
지금까지 공부한 검색 알고리즘은 배열의 요소를 데이터 수만큼만 준비했다. 해시탐색법은 이와 달리 데이터의 1.5~2배를 준비해야 한다.

임시 배열(arrayD)의 첫번째 요소0부터 순차적으로 해시 값을 계산하여 arrayH로 저장한다. 준비한 arrayH의 요소가 11이므로 addrayD의 데이터를 11로 나눈 나머지를 계산하는 방식을 사용한다.

arrayH[1]에 이미 다른 데이터가 할당되어 있는 확인한 후 비어 있으면 이곳에 저장한다. 왜 확인할 필요가 있는지 더 자세히 추후에 설명하겠지만 저장할 요소들이 많아지면 해시값 우연히 일치하는 경우가 발생하게 된다. 저장하고 자 하는 위치에 이미 데이터가 저장되어있을 가능성이 있다. 요소가 비어 있는지 확인하려면 arrayH[1]의 값이 0인지 여부를 확인하면된다. (0으로 이미 초기화 하였다.) 비어있으면 즉 0이면 대입한다. No 어떤 값이 이미 있는 경우의 처리는 뒤에서 따로 알아보자.

문제

아래 알고리즘을 보고, 파이썬 코드를 작성해보자!

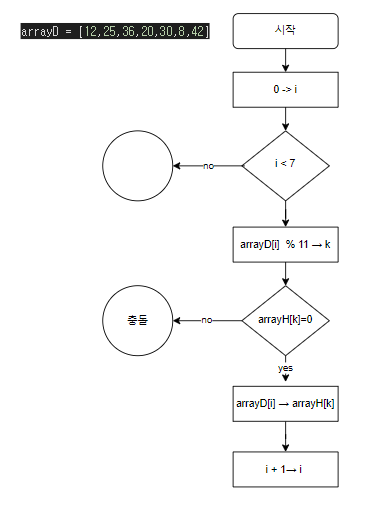
arrayD = [12,25,36,20,30,8,42]
arrayH = [0] * 11 
i = 0

while i < 7:
  k =  arrayD[0]  % 11        # 해시함수

  if arrayH[k] == 0:          # 칸에 이미 들어가 있는 값이 없으면
    arrayD[0] = arrayH[k]    # 집어 넣어라
  i = i + 1

  else :
# 12 -> 1
# 25 -> 3
# 36 -> 3 (충돌)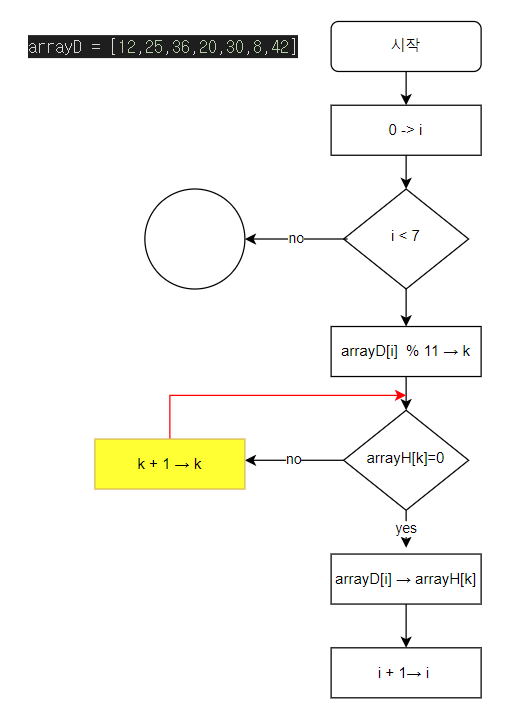

arrayD = [12,25,36,20,30,8,42]
arrayH = [0] * 11 
i = 0

while i < 7:
  k =  arrayD[0]  % 11        # 해시함수

  if arrayH[k] == 0:          # 칸에 이미 들어가 있는 값이 없으면
    arrayD[0] = arrayH[k]    # 집어 넣어라
  i = i + 1

  else :
    k = k + 1
    continue

  i = i + 1

  else
# 12 -> 1
# 25 -> 3
# 36 -> 3 (충돌)

충돌이 너무 빈번하게 일어나면 추가 처리작업 많이 발생된다. 이로 인해 한번에 데이터를 검색할수 있다는 해시 탐색법의 장점이 무색해진다. 충돌이 많이 일어나지 않게 하려면 해시함수를 잘 고안아혀 가능한 한 흩어지도록 해야한다. 또다른 해결책은 배열의 요소를 많이 준비하는 방법이다. 요소 수가 많을 수록 충돌의 가능성은 적어지지만 메모리 사용량이 늘어나기 때문에 알고리즘의 효율성이 떨어진다. 탐색 처리의 속도를 유지하는 것과 메모리를 적게 사용하는 요소수는 일반적으로 저장 데이터 수의 1.5~ 2배 라고 연구되고 있다.

# 12 -> 1
# 25 -> 3
# 36 -> 3 (충돌) -> 4
# 20 -> 9
# 30 -> 8
# 8  -> 8 (충돌) -> 9 (충돌) -> 10
# 42 -> 9 (충돌) -> 10(충돌) -> 11

'''
k가 10을 초과했을 때의 대응을 조건식으로 나누어 처리를 추가할 수도 있지만 코드가 복잡해진다. 좀 더 간단한 방법을 찾아보자.
'''

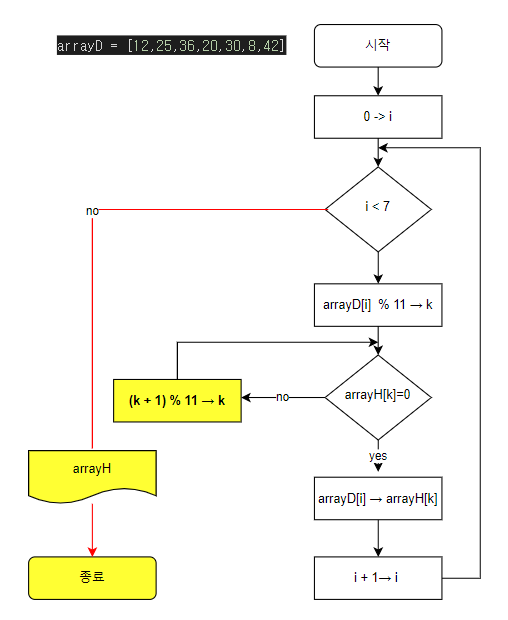
arrayD = [12,25,36,20,30,8,42]
arrayH = [0] * 11 
i = 0
k =  arrayD[i]  % 11        # 해시함수

while i < 7:
  k = arrayD[i] % 11

  while True:
    if arrayH[k] == 0:          # 칸에 이미 들어가 있는 값이 없으면
      arrayH[k] = arrayD[i]     # 집어 넣어라
      break
    else:
      k = (k + 1) % 11
      # print(k)
      continue

  i = i + 1

print(arrayH)

출력 답: [42, 12, 0, 25, 36, 0, 0, 0, 30, 20, 8]

Algorithms